1505  GPS and Outdoor Positioning

1505.1 Learning Objectives

By the end of this chapter, you will be able to:

  • Explain GPS/GNSS Architecture: Understand the space, control, and user segments of satellite navigation systems
  • Calculate Positioning from Satellites: Apply Time of Flight and TDoA principles to determine position
  • Identify Multipath Effects: Recognize how signal reflections degrade positioning accuracy
  • Understand Clock Synchronization: Explain why atomic clocks are essential and how pseudoranges work

1505.2 Prerequisites

1505.4 Time of Flight (ToF)

Time of Flight: Measure the time taken for a signal to propagate from transmitter to receiver.

%% fig-cap: "Time of Flight (ToF) Positioning Concept"
%% fig-alt: "Diagram showing Time of Flight positioning with signal transmission and distance calculation"

%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ecf0f1', 'noteTextColor': '#2C3E50', 'noteBkgColor': '#fff3cd', 'textColor': '#2C3E50', 'fontSize': '16px'}}}%%

graph LR
    Tx[Transmitter<br/>Satellite<br/>Time: T1]

    Tx -->|Signal travels at<br/>c = 299,792,458 m/s| Signal[RF Signal<br/>Time of Flight<br/>Δt = T2 - T1]

    Signal --> Rx[Receiver<br/>GPS Device<br/>Time: T2]

    Rx --> Calc[Distance Calculation<br/>d = c × Δt<br/>d = c × T2 - T1]

    Calc --> Result[Distance Result<br/>e.g., 20,000 km]

    subgraph Problem["Critical Challenge"]
        Sync[Clock Synchronization<br/>Required!<br/>1 μs error = 300m<br/>1 ns error = 0.3m]
    end

    style Tx fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style Signal fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Rx fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style Calc fill:#2C3E50,stroke:#16A085,stroke-width:2px,color:#fff
    style Result fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style Sync fill:#E67E22,stroke:#16A085,stroke-width:3px,color:#fff

Figure 1505.2: Diagram showing Time of Flight positioning with critical clock synchronization requirement.
Diagram illustrating Time of Flight (ToF) positioning concept showing signal transmission from transmitter to receiver with timing markers and distance calculation formula d = c × Δt
Figure 1505.3: Time of Flight Concept

Distance Calculation:

Distance = Speed of Light × Time of Flight
d = c × Δt

where:
- c = 299,792,458 m/s (speed of light in vacuum)
- Δt = reception time - transmission time

Critical Challenge: Both transmitter and receiver must have synchronized clocks to know the true transmission time.

Synchronization Sensitivity:

1 microsecond clock error = 300 meters position error!
1 nanosecond clock error = 0.3 meters position error

1505.5 The Multipath Problem

Diagram showing multipath propagation where GPS signals travel multiple paths to receiver by reflecting off buildings and surfaces, creating measurement errors in position calculation
Figure 1505.4: Multipath problem in GPS

Multipath: Signals reflect off objects, creating multiple paths between transmitter and receiver.

%% fig-cap: "Multipath Propagation Effects on Positioning"
%% fig-alt: "Diagram illustrating multipath propagation where GPS signals take multiple paths to reach receiver"

%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ecf0f1', 'noteTextColor': '#2C3E50', 'noteBkgColor': '#fff3cd', 'textColor': '#2C3E50', 'fontSize': '16px'}}}%%

graph TD
    Sat[GPS Satellite<br/>Transmitter]

    Sat -->|Direct Path<br/>True Distance| Direct[Receiver<br/>Line-of-Sight<br/>d = 20,000 km]

    Sat -->|Reflected Path 1<br/>Longer Distance| B1[Building]
    B1 --> Reflect1[Receiver<br/>Reflected Signal<br/>d = 20,100 km]

    Sat -->|Reflected Path 2<br/>Longer Distance| B2[Building]
    B2 --> Ground[Ground]
    Ground --> Reflect2[Receiver<br/>Multiple Bounces<br/>d = 20,200 km]

    subgraph Impact["Multipath Impact"]
        Comm[Communications:<br/>Multiple signals combine<br/>Improves reception]
        Pos[Positioning:<br/>Distances appear longer<br/>Position errors]
        Indoor[Indoor:<br/>Severe multipath<br/>GPS fails]
    end

    style Sat fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style Direct fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style Reflect1 fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Reflect2 fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style B1 fill:#7F8C8D,stroke:#2C3E50,stroke-width:2px,color:#fff
    style B2 fill:#7F8C8D,stroke:#2C3E50,stroke-width:2px,color:#fff

Figure 1505.5: Diagram illustrating multipath propagation where GPS signals take multiple paths to reach receiver.

Impact: - Fine for communications: Multiple signals can be combined - Kills positioning: Makes distances appear longer than reality - Indoor environments: Severe multipath due to many reflective surfaces

1505.6 Time Difference of Arrival (TDoA)

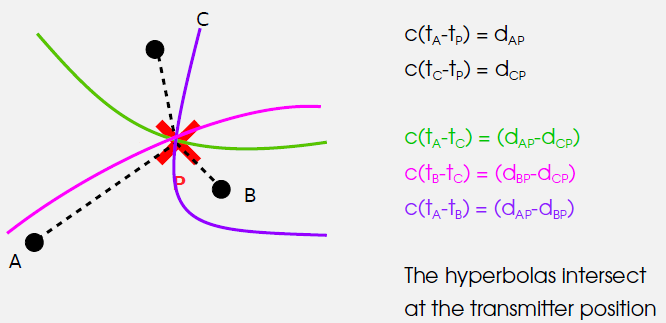
Diagram illustrating Time Difference of Arrival (TDoA) positioning where multiple synchronized base stations measure arrival time differences from a transmitter to determine its location without requiring clock synchronization at the mobile device
Figure 1505.6: Time difference of arrival

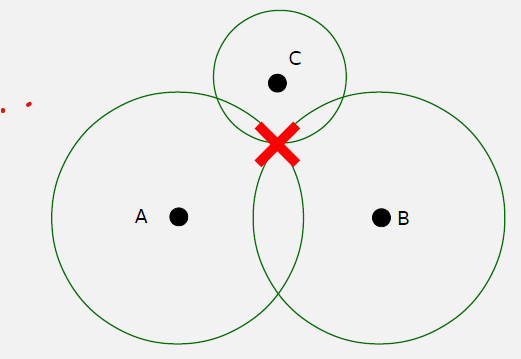
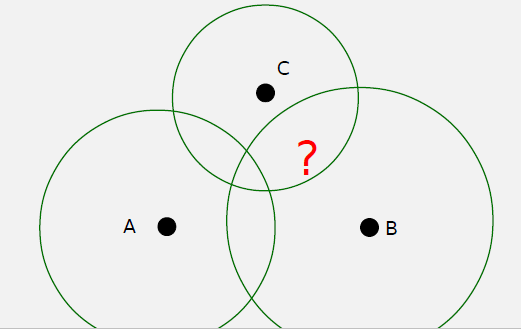
The Problem with Simple ToF: - Mobile device and fixed sites separated by large distances - Cannot keep clocks synchronized - RF signals travel at c, so 1 μs sync error = 300m position error

TDoA Solution: - Accept that clocks aren’t synced - Solve for the clock offset as an additional unknown - Any single range is wrong, but every range is wrong by the same amount - These erroneous ranges are called pseudoranges

%% fig-cap: "Time Difference of Arrival (TDoA) Positioning System"
%% fig-alt: "Diagram showing TDoA positioning system architecture with synchronized base stations"

%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ecf0f1', 'noteTextColor': '#2C3E50', 'noteBkgColor': '#fff3cd', 'textColor': '#2C3E50', 'fontSize': '16px'}}}%%

graph TB
    Mobile[Mobile Device<br/>Unsynchronized Clock<br/>Clock offset = unknown]

    Mobile -->|Signal| BS1[Base Station 1<br/>Synchronized<br/>Receives at T1]
    Mobile -->|Signal| BS2[Base Station 2<br/>Synchronized<br/>Receives at T2]
    Mobile -->|Signal| BS3[Base Station 3<br/>Synchronized<br/>Receives at T3]
    Mobile -->|Signal| BS4[Base Station 4<br/>Synchronized<br/>Receives at T4]

    BS1 --> Calc[TDoA Calculation]
    BS2 --> Calc
    BS3 --> Calc
    BS4 --> Calc

    Calc --> TD1[Time Difference:<br/>T2 - T1 = ΔT12]
    Calc --> TD2[Time Difference:<br/>T3 - T1 = ΔT13]
    Calc --> TD3[Time Difference:<br/>T4 - T1 = ΔT14]

    TD1 --> Position[Position Calculation<br/>4 unknowns:<br/>x, y, z, clock offset<br/>Need 4+ base stations]

    TD2 --> Position
    TD3 --> Position

    subgraph Key["Key Advantage"]
        Adv[Mobile clock can be wrong!<br/>Offset solved as unknown<br/>Pseudoranges all wrong<br/>by same amount]
    end

    style Mobile fill:#E67E22,stroke:#16A085,stroke-width:3px,color:#fff
    style BS1 fill:#2C3E50,stroke:#16A085,stroke-width:2px,color:#fff
    style BS2 fill:#2C3E50,stroke:#16A085,stroke-width:2px,color:#fff
    style BS3 fill:#2C3E50,stroke:#16A085,stroke-width:2px,color:#fff
    style BS4 fill:#2C3E50,stroke:#16A085,stroke-width:2px,color:#fff
    style Calc fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style Position fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style Adv fill:#E67E22,stroke:#16A085,stroke-width:3px,color:#fff

Figure 1505.7: Diagram showing TDoA positioning system architecture with mobile device and synchronized base stations.

Key Requirements for TDoA:

  1. Base Stations Must Be Synchronized:
    • Lay cables between stations
    • Use GPS (ironically!)
    • Give them all atomic clocks ($$$)
  2. Mobile Device Clock Can Be Wrong:
    • Clock offset becomes an additional unknown to solve
    • Need N+1 stations for N-dimensional positioning
    • 3D position + clock offset = 4 unknowns → need 4 satellites

1505.7 GPS Architecture

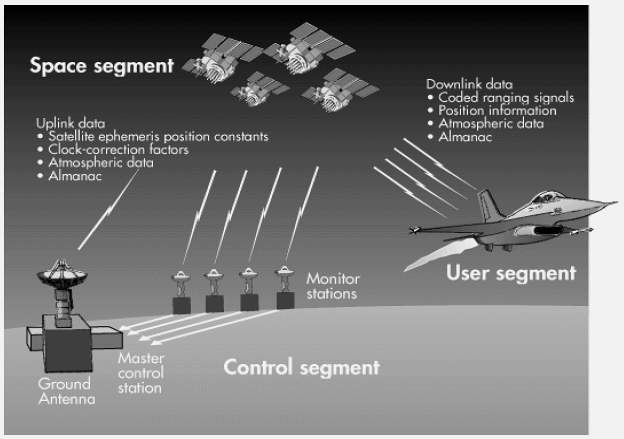
Overview of GPS system architecture showing the three segments: space segment with satellites, control segment with ground stations, and user segment with GPS receivers
Figure 1505.8: GPS System Overview 

%% fig-cap: "GPS System Architecture - Three Segments"
%% fig-alt: "Complete GPS system architecture showing three interconnected segments"

%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ecf0f1', 'noteTextColor': '#2C3E50', 'noteBkgColor': '#fff3cd', 'textColor': '#2C3E50', 'fontSize': '16px'}}}%%

graph TB
    subgraph Space["Space Segment"]
        S1[31 GPS Satellites<br/>6 orbital planes<br/>MEO: 20,200 km]
        S2[Atomic Clocks<br/>Caesium/Rubidium<br/>±1 ns/day accuracy]
        S3[Signal Transmission<br/>L1: 1575 MHz<br/>L2: 1227 MHz<br/>L5: 1176 MHz]
    end

    subgraph Control["Control Segment"]
        C1[Master Control Station<br/>Schriever AFB, Colorado]
        C2[Monitor Stations<br/>Worldwide tracking]
        C3[Upload ephemeris<br/>Clock corrections<br/>Orbit adjustments]
    end

    subgraph User["User Segment"]
        U1[GPS Receivers<br/>Smartphones, vehicles<br/>IoT devices, drones]
        U2[Position Calculation<br/>Trilateration from<br/>4+ satellites]
        U3[Applications<br/>Navigation, tracking<br/>timing, surveying]
    end

    S1 -->|Broadcast signals| U1
    S3 -->|L1/L2/L5 signals| U1
    C2 -->|Monitor orbits<br/>Clock drift| C1
    C1 -->|Upload corrections| S1
    C3 -->|Ephemeris data| S1
    U1 --> U2
    U2 --> U3

    style S1 fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style C1 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style U1 fill:#E67E22,stroke:#16A085,stroke-width:3px,color:#fff
    style U2 fill:#2C3E50,stroke:#16A085,stroke-width:2px,color:#fff

Figure 1505.9: Complete GPS system architecture showing three interconnected segments.

GPS is TDoA (Inverted):

  • Satellites play the part of static devices (but are transmitters)
  • Mobile device measures reception time using its clock
  • Uses satellite’s transmitted time for the time difference
  • For each satellite: measures (ToF + c × clockOffset)
  • These are pseudoranges (erroneous distances)

1505.8 Satellite Synchronization

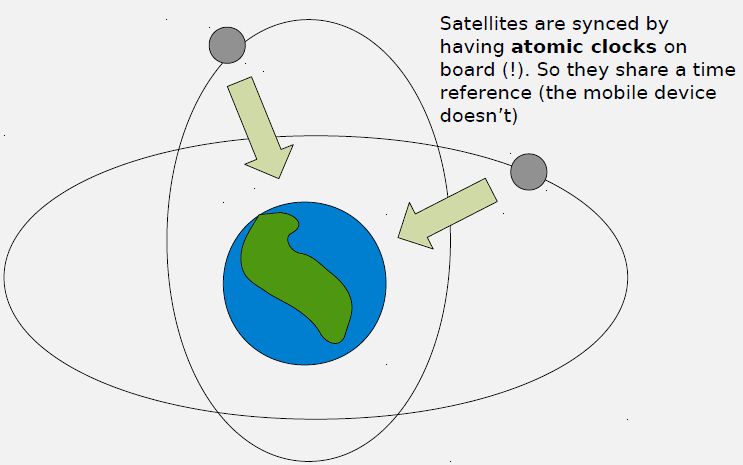
Diagram explaining GPS satellite synchronization mechanisms using onboard atomic clocks, ground control monitoring, and correction uploads to maintain precise timing across the constellation
Figure 1505.10: How are satellites synced

How Satellites Stay Synchronized:

  1. Atomic Clocks On Board (Caesium or Rubidium)
    • Cost: ~$100,000 per clock
    • Accuracy: ~1 nanosecond per day
    • All satellites share time reference
  2. But They Aren’t Static?
    • True! But we know their orbits precisely
    • Can predict positions quite accurately
    • Small errors do creep in…
  3. Ground Control Segment:
    • Dedicated ground stations monitor satellite orbits
    • Track actual positions vs predicted
    • Upload corrections to satellites
    • Must model relativistic effects!
Illustration of ground control segment monitoring satellite orbits, tracking positions, and uploading corrections including relativistic time adjustments
Figure 1505.11: Satellite Orbit Monitoring

Relativistic Effects: - Special Relativity: Satellite clocks run slower due to velocity (~7 μs/day slower) - General Relativity: Satellite clocks run faster due to weaker gravity (~45 μs/day faster) - Net Effect: ~38 μs/day faster → must be corrected!

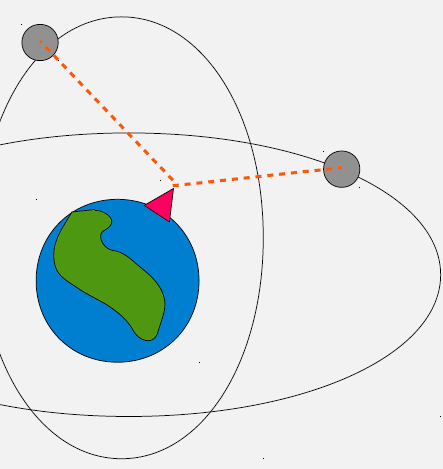
1505.9 GPS Position Calculation

Mathematical representation of GPS position calculation equations showing pseudorange formulas with satellite coordinates, receiver position unknowns, and clock offset variables
Figure 1505.12: GPS position calculation 

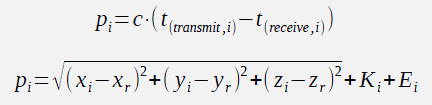
%% fig-cap: "GPS Position Calculation Process"
%% fig-alt: "Flowchart showing GPS position calculation from pseudoranges to final position"

%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ecf0f1', 'noteTextColor': '#2C3E50', 'noteBkgColor': '#fff3cd', 'textColor': '#2C3E50', 'fontSize': '16px'}}}%%

graph TB
    Start[GPS Receiver]

    Start --> Measure[Measure Pseudoranges<br/>ρ1, ρ2, ρ3, ρ4<br/>to 4+ satellites]

    Measure --> Ephemeris[Get Satellite Positions<br/>x1,y1,z1 ... x4,y4,z4<br/>from ephemeris data]

    Ephemeris --> Equations[4 Equations<br/>4 Unknowns]

    subgraph Unknowns["4 Unknowns to Solve"]
        U1[xr - receiver X]
        U2[yr - receiver Y]
        U3[zr - receiver Z]
        U4[Δt - clock offset]
    end

    Equations --> Solve[Solve Simultaneous<br/>Equations<br/>Iterative algorithm]

    Solve --> Correct[Apply Corrections<br/>Ionospheric delay<br/>Tropospheric delay<br/>Satellite clock errors]

    Correct --> Position[Final Position<br/>Latitude, Longitude<br/>Altitude<br/>±5-10m accuracy]

    subgraph Formula["Pseudorange Formula"]
        F[ρi = √x-xi² + y-yi² + z-zi² + c·Δt]
    end

    style Start fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style Equations fill:#E67E22,stroke:#16A085,stroke-width:3px,color:#fff
    style Solve fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style Position fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style Formula fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff

Figure 1505.13: Flowchart showing GPS position calculation process.

Position Equations:

For each satellite \(i\):

\[ \rho_i = \sqrt{(x_i - x_r)^2 + (y_i - y_r)^2 + (z_i - z_r)^2} + c \cdot \Delta t + E_i \]

Where: - \(\rho_i\) = pseudorange to satellite \(i\) (measured) - \((x_i, y_i, z_i)\) = satellite \(i\) position (known from ephemeris) - \((x_r, y_r, z_r)\) = receiver position (unknown) - \(c\) = speed of light - \(\Delta t\) = receiver clock offset (unknown) - \(E_i\) = error term (atmospheric delays, etc.)

Four Unknowns: 1. \(x_r\) (receiver X position) 2. \(y_r\) (receiver Y position) 3. \(z_r\) (receiver Z position) 4. \(\Delta t\) (clock offset)

Need at least 4 satellites to solve for 4 unknowns!

1505.10 GPS Error Sources

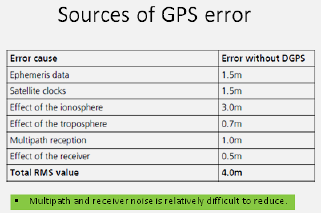
Comprehensive diagram showing various GPS error sources including ionospheric delay, tropospheric delay, multipath interference, satellite clock drift, ephemeris inaccuracies, and receiver noise, with typical error magnitude ranges for each
Figure 1505.14: GPS error sources

Signal Strength Challenge: - GPS signal transmitted at 20 watts - Travels 12,500 miles (20,000 km) - Received power: ~10^-16 watts (incredibly weak!) - Various atmospheric effects introduce errors

%% fig-cap: "GPS Error Sources and Magnitudes"
%% fig-alt: "Comprehensive breakdown of GPS error sources with typical magnitudes and mitigations"

%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ecf0f1', 'noteTextColor': '#2C3E50', 'noteBkgColor': '#fff3cd', 'textColor': '#2C3E50', 'fontSize': '16px'}}}%%

graph TB
    GPS[GPS Position<br/>Calculation]

    GPS --> Errors{Error Sources}

    Errors --> Ion[Ionospheric Delay<br/>±5 meters<br/>Refraction in<br/>ionosphere]
    Errors --> Trop[Tropospheric Delay<br/>±0.5 meters<br/>Water vapor,<br/>temperature]
    Errors --> Clock[Satellite Clock<br/>±2 meters<br/>Atomic clock drift]
    Errors --> Eph[Ephemeris Error<br/>±2.5 meters<br/>Orbit prediction<br/>inaccuracy]
    Errors --> Multi[Multipath<br/>±1 meter<br/>Signal reflections]
    Errors --> Noise[Receiver Noise<br/>±0.3 meters<br/>Electronics,<br/>antenna quality]

    Ion --> Mit1[Mitigation:<br/>Dual-frequency<br/>receivers]
    Trop --> Mit2[Mitigation:<br/>Atmospheric<br/>modeling]
    Clock --> Mit3[Mitigation:<br/>Ground station<br/>corrections]
    Eph --> Mit4[Mitigation:<br/>Frequent ephemeris<br/>updates]
    Multi --> Mit5[Mitigation:<br/>Antenna design,<br/>signal averaging]
    Noise --> Mit6[Mitigation:<br/>Better receivers,<br/>filtering]

    Mit1 --> Total[Total Error<br/>5-10 meters<br/>civilian GPS]
    Mit2 --> Total
    Mit3 --> Total
    Mit4 --> Total
    Mit5 --> Total
    Mit6 --> Total

    style GPS fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style Errors fill:#E67E22,stroke:#16A085,stroke-width:3px,color:#fff
    style Ion fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Trop fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Clock fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Eph fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Multi fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Noise fill:#E67E22,stroke:#16A085,stroke-width:2px,color:#fff
    style Total fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff

Figure 1505.15: Comprehensive breakdown of GPS error sources with mitigation strategies.
Error Source Typical Error Mitigation
Ionospheric delay ±5 m Dual-frequency correction
Tropospheric delay ±0.5 m Modeling
Satellite clock ±2 m Ground station corrections
Ephemeris ±2.5 m Frequent updates
Multipath ±1 m Antenna design, averaging
Receiver noise ±0.3 m Better receivers

1505.11 Knowledge Check

Question 1: Why does GPS require at least 4 satellites to calculate a position?

GPS position calculation involves 4 unknowns: the receiver’s 3D position (x, y, z) plus the receiver’s clock offset from GPS time. Each satellite provides one pseudorange equation, so we need at least 4 equations to solve for 4 unknowns. Additional satellites can improve accuracy through overdetermined solutions but aren’t strictly required.

Question 2: What is a “pseudorange” in GPS terminology?

A pseudorange is the measured distance to a satellite, which includes the actual geometric distance plus an error term caused by the receiver’s clock offset from GPS time. Since all pseudoranges are affected by the same clock offset, the offset can be solved as an additional unknown in the position calculation.

Question 3: Why is 1 microsecond of clock error equivalent to 300 meters of position error?

GPS positioning uses time-of-flight ranging where distance = speed of light × time. The speed of light is approximately 300,000 km/s (or 300 meters per microsecond). Therefore, a 1 microsecond timing error translates directly to a 300 meter distance error. This is why atomic clocks are essential for GPS satellites.

1505.12 What’s Next

Continue to GPS Accuracy and Enhancement to learn about the GPS error budget, differential GPS corrections, and RTK techniques that achieve centimeter-level accuracy for precision applications.