%% fig-alt: "Ad hoc network topology showing 8 nodes (A through H) connected in mesh configuration. Node D highlighted in orange as reference point. Connections: A-B, B-C, B-D, D-F, F-E, F-H, E-G. Demonstrates multi-hop paths with Node D having two gateway neighbors (B and F) for reaching different network segments."
%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#7F8C8D'}}}%%
graph TB
A[Node A] --- B[Node B]
B --- C[Node C]
B --- D[Node D]
D --- F[Node F]
F --- E[Node E]
F --- H[Node H]
E --- G[Node G]
style A fill:#16A085,stroke:#2C3E50,color:#fff
style B fill:#16A085,stroke:#2C3E50,color:#fff
style C fill:#16A085,stroke:#2C3E50,color:#fff
style D fill:#E67E22,stroke:#2C3E50,color:#fff
style E fill:#16A085,stroke:#2C3E50,color:#fff
style F fill:#16A085,stroke:#2C3E50,color:#fff
style G fill:#16A085,stroke:#2C3E50,color:#fff
style H fill:#16A085,stroke:#2C3E50,color:#fff
246 DSDV Fundamentals: Proactive Routing Tables
246.1 Learning Objectives
By the end of this chapter, you will be able to:
- Understand DSDV Protocol: Explain Destination-Sequenced Distance Vector as a proactive routing protocol
- Analyze Routing Tables: Describe how nodes maintain complete routing tables for all destinations
- Apply Sequence Numbers: Use sequence numbers to prevent routing loops and select fresh routes
- Evaluate Route Selection: Determine optimal routes based on sequence numbers and hop counts
246.2 Prerequisites
Before diving into this chapter, you should be familiar with:
- Ad Hoc Fundamentals: Core concepts of ad hoc networking including self-organization, infrastructure-less operation, and peer-to-peer communication
- Multi-hop Fundamentals: Understanding multi-hop routing concepts and path establishment
- Networking Basics: Fundamental networking concepts including routing tables, hop counts, packet forwarding, and distance-vector algorithms
- Routing Fundamentals: General routing principles, including path selection, routing metrics, and loop prevention
Imagine you’re planning a road trip and want to know the best route to every city in your country. You could either (1) keep an always-updated map showing routes to everywhere, or (2) only look up directions when you actually decide to visit a specific city. Proactive routing (DSDV) is like option 1 - always maintaining routes even before you need them.
Proactive = Always Ready
Think of DSDV like a GPS that constantly updates routes to all destinations: - Pro: When you want to go somewhere, the route is immediately available (zero delay) - Con: Your GPS is constantly working and draining battery updating routes you may never use
How DSDV Works: The Phone Book Analogy
Every node maintains a “phone book” (routing table) listing how to reach every other node:
My Routing Table (Node D):
To reach Node A: Send to neighbor B (2 hops away)
To reach Node F: Send to neighbor F (1 hop away)
To reach Node G: Send to neighbor F (3 hops away)Periodic Updates - The Gossip Network:
Every 15 seconds, nodes broadcast their routing tables to neighbors (like gossiping about who lives where). When you hear an update: 1. If it’s a new destination, add it to your table 2. If it’s a shorter path to known destination, update your table 3. If it’s the same destination via longer path, ignore it
Sequence Numbers - The Freshness Date:
Problem: What if a route is outdated (road closed)? DSDV uses sequence numbers like expiration dates on food: - Higher sequence number = fresher information - Always trust fresher routes, even if they’re longer - Example: Route with seq#42 and 5 hops beats route with seq#40 and 2 hops (fresher wins!)
| Term | Simple Explanation | Everyday Analogy |
|---|---|---|
| Proactive Routing | Maintain routes continuously before needed | Always-updated GPS |
| Routing Table | List of how to reach all destinations | Phone book with addresses |
| Hop Count | Number of intermediate nodes on path | Number of stops on bus route |
| Sequence Number | Freshness indicator for route | Expiration date on milk |
| Distance Vector | Share hop-count info with neighbors | Tell neighbors how far cities are |
| Periodic Update | Regularly broadcast routing info | Weekly neighborhood newsletter |
246.3 What is DSDV?
Destination-Sequenced Distance-Vector (DSDV) is a proactive (table-driven) routing protocol where each node maintains a complete routing table with entries for all network destinations.
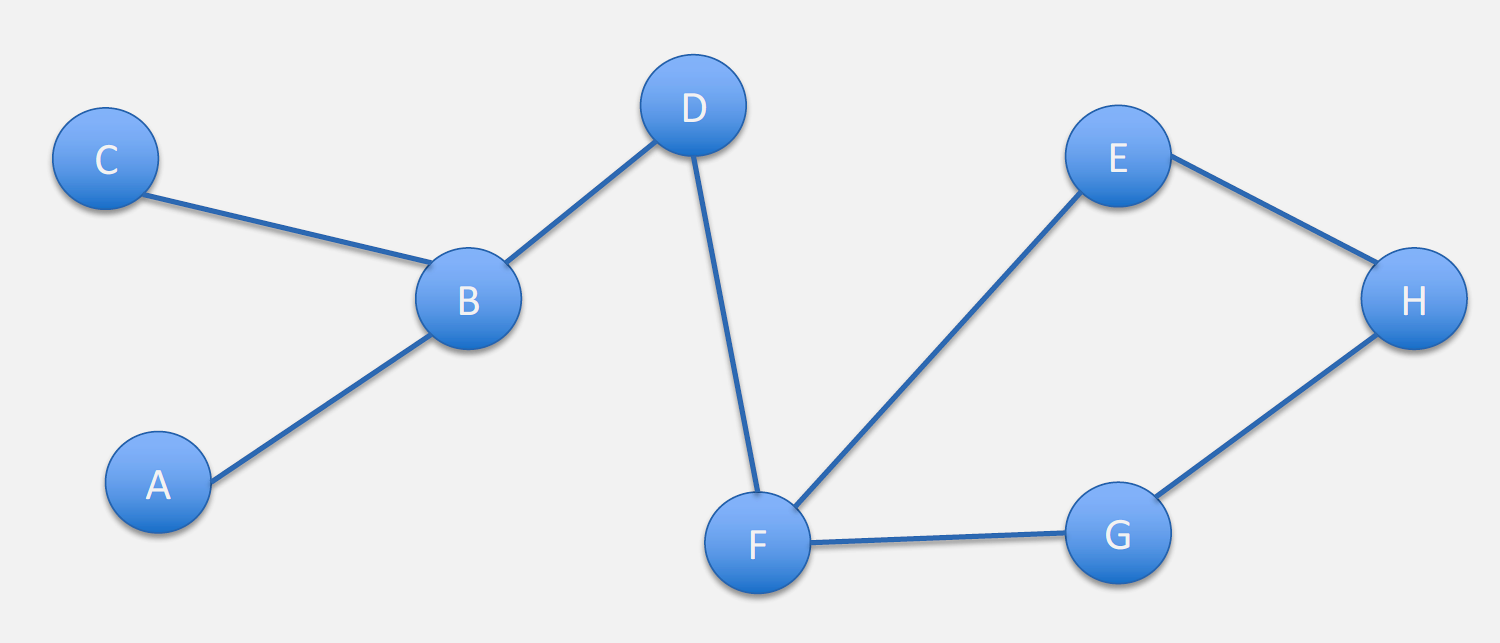
246.3.1 Proactive Routing Characteristics
- Proactive protocols:
- Maintain routes to all destinations continuously, even when not actively communicating
Key Characteristics: - Routes always available (no discovery delay) - Periodic route updates broadcast throughout network - Higher overhead (continuous maintenance traffic) - Good for networks where most nodes communicate frequently
246.3.2 DSDV Routing Table Structure
Each node maintains a table with entries:
| Destination | Next Hop | Hops | Seq # |
|---|---|---|---|
| Node A | Node B | 2 | 42 |
| Node C | Node C | 1 | 17 |
| Node D | Node B | 3 | 38 |
Fields: - Destination: Target node address - Next Hop: Immediate neighbor to forward packet to - Hops Required: Distance metric (hop count) - Destination Sequence Number: Freshness indicator assigned by destination
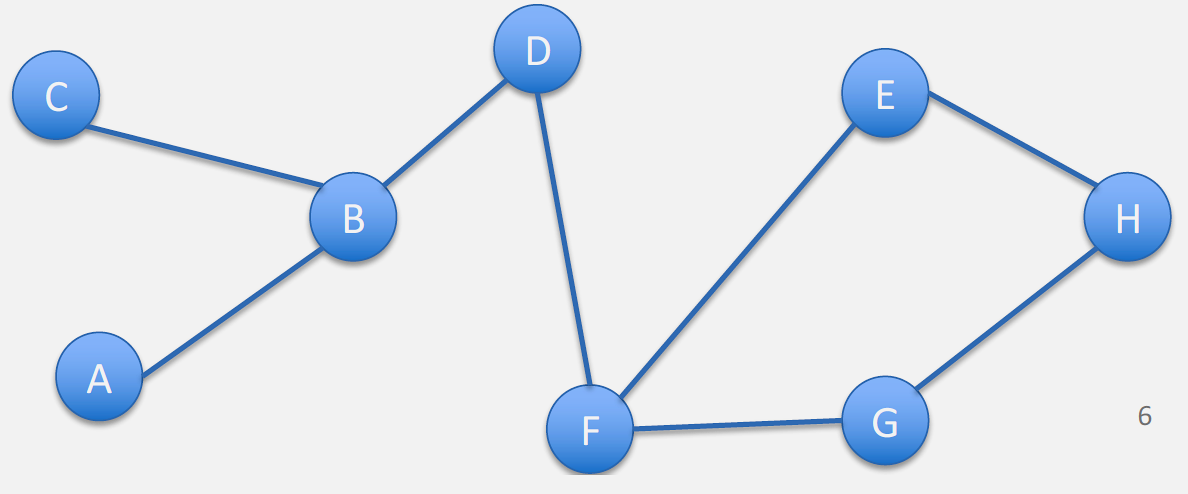
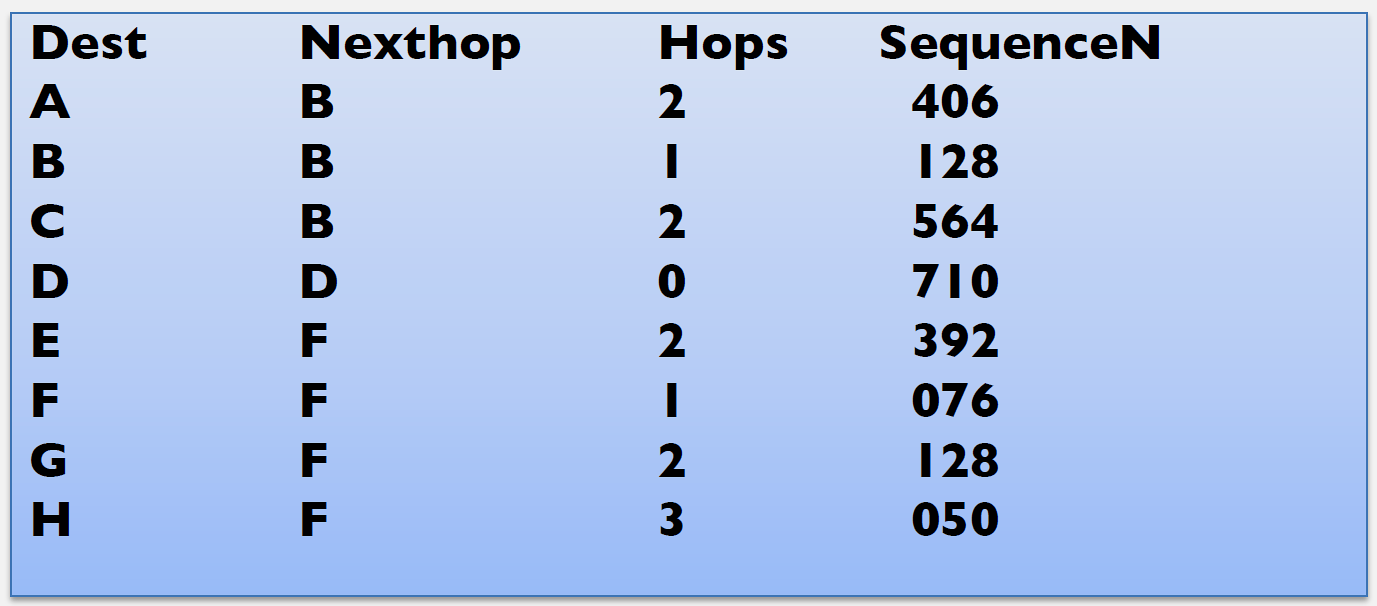
246.4 Example Network Topology
Consider this ad hoc network:
246.4.1 Node D’s Routing Table
| Destination | Next Hop | Hops | Seq # | Route |
|---|---|---|---|---|
| A | B | 2 | 042 | D-B-A |
| B | B | 1 | 156 | D-B |
| C | B | 2 | 234 | D-B-C |
| E | F | 2 | 392 | D-F-E |
| F | F | 1 | 076 | D-F |
| G | F | 3 | 128 | D-F-E-G |
| H | F | 2 | 050 | D-F-H |
%% fig-alt: "Node D's DSDV routing table visualization showing routes to 7 destinations. Central node D (orange) connects to destinations via two next-hop neighbors: Node B (routes to A, B, C with 1-2 hops) and Node F (routes to E, F, G, H with 1-3 hops). Demonstrates distance-vector routing with hop-count metrics."
%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#7F8C8D'}}}%%
graph TB
subgraph Routes["Node D's Routes"]
D[Node D<br/>Routing Table] -->|Next: B, 2 hops| A[To Node A]
D -->|Next: B, 1 hop| B[To Node B]
D -->|Next: B, 2 hops| C[To Node C]
D -->|Next: F, 2 hops| E[To Node E]
D -->|Next: F, 1 hop| F[To Node F]
D -->|Next: F, 3 hops| G[To Node G]
D -->|Next: F, 2 hops| H[To Node H]
end
style D fill:#E67E22,stroke:#2C3E50,color:#fff
style A fill:#16A085,stroke:#2C3E50,color:#fff
style B fill:#16A085,stroke:#2C3E50,color:#fff
style C fill:#16A085,stroke:#2C3E50,color:#fff
style E fill:#16A085,stroke:#2C3E50,color:#fff
style F fill:#16A085,stroke:#2C3E50,color:#fff
style G fill:#16A085,stroke:#2C3E50,color:#fff
style H fill:#16A085,stroke:#2C3E50,color:#fff
246.4.2 Route Selection Decision Process
%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#7F8C8D'}}}%%
flowchart TB
subgraph NodeD["Node D - Routing Decision"]
PKT["Packet for<br/>Destination G"]
TABLE["Routing Table<br/>Lookup"]
ENTRY["Entry Found:<br/>G via F, 3 hops, seq=128"]
FWD["Forward to<br/>Neighbor F"]
end
subgraph PathViaB["Path via B (Not Selected)"]
B_ROUTE["D - B - A - ?<br/>No route to G via B"]
end
subgraph PathViaF["Path via F (Selected)"]
F_ROUTE["D - F - E - G<br/>3 hops, current"]
end
PKT --> TABLE
TABLE --> ENTRY
ENTRY --> FWD
FWD -.->|"Rejected"| B_ROUTE
FWD ==>|"Selected"| F_ROUTE
style NodeD fill:#E67E22,color:#fff
style PathViaB fill:#7F8C8D,color:#fff
style PathViaF fill:#16A085,color:#fff
style FWD fill:#2C3E50,color:#fff
246.5 DSDV Route Updates
Nodes exchange routing information periodically or when topology changes.
Update Message Format:
<Destination, Next Hop, Hop Count, Sequence Number>Route Selection Rules:
- Prefer fresher routes: If sequence numbers differ, choose higher sequence number
- Prefer shorter routes: If sequence numbers equal, choose lower hop count
- Update on change: Broadcast updates when topology changes
%%{init: {'theme': 'base', 'themeVariables': { 'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#7F8C8D'}}}%%
sequenceDiagram
participant N as Network
participant A as Node A
participant B as Node B
participant D as Node D
Note over N,D: t=0s: Initial State
rect rgb(44, 62, 80)
Note right of A: A: seq=40
Note right of B: B: seq=150
Note right of D: D: seq=35
end
Note over N,D: t=15s: Periodic Update Cycle
A->>B: Broadcast: <A,A,0,42>
B->>A: Broadcast: <B,B,0,156>
B->>D: Broadcast: <B,B,0,156>
D->>B: Broadcast: <D,D,0,38>
Note over N,D: t=30s: Routes Propagate
B->>D: <A,B,1,42>
D->>B: <A,B,2,42> via D
Note over D: D learns route to A:<br/>Next=B, Hops=2, Seq=42
Note over N,D: t=45s: Link Failure D-F
rect rgb(231, 76, 60)
Note over D: Link D-F timeout!<br/>Mark F routes as infinity<br/>Increment seq: 76 to 77
end
D->>B: <F,inf,77> BROKEN ROUTE
B->>A: <F,inf,77> BROKEN ROUTE
Note over A,D: All nodes remove D-F routes
246.6 Sequence Number Mechanism
The sequence number is DSDV’s key innovation that distinguishes it from traditional distance-vector protocols.
246.6.1 Why Sequence Numbers Matter
In traditional distance-vector routing (like RIP), the “count-to-infinity” problem occurs when a link fails:
- Node A loses route to destination X
- Node B still has stale route “to X via A, 2 hops”
- A asks B for route, gets “via B, 3 hops” (B thinks via A works)
- B asks A for route, gets “via A, 4 hops” (A thinks via B works)
- Hop count keeps increasing until reaching infinity threshold
DSDV solves this with sequence numbers:
- Each destination generates its own sequence numbers (even numbers)
- When a route breaks, intermediate nodes increment sequence number (to odd)
- Higher sequence number always wins, regardless of hop count
- Stale routes are immediately identified and discarded
246.6.2 Route Selection Algorithm
if (new_seq_number > current_seq_number):
# Fresher route - always adopt
update_route(new_route)
elif (new_seq_number == current_seq_number):
if (new_hop_count < current_hop_count):
# Same freshness, shorter path
update_route(new_route)
else:
# Stale route - discard
ignore(new_route)246.7 Knowledge Check
246.8 Summary
This chapter covered the fundamentals of DSDV (Destination-Sequenced Distance Vector) proactive routing:
- Proactive Nature: DSDV maintains complete routing tables to all destinations continuously, enabling immediate packet forwarding without discovery delays
- Routing Table Structure: Each node stores destination, next hop, hop count, and sequence number for every network destination
- Sequence Numbers: The key innovation that ensures route freshness and prevents routing loops by always preferring higher sequence numbers
- Route Selection: Prioritizes freshness (sequence number) over efficiency (hop count) to guarantee correctness
- Periodic Updates: Nodes broadcast routing tables regularly to maintain network-wide consistency
Continue to DSDV Protocol Operation to learn how DSDV handles topology changes including new node joins, link breaks, and route convergence mechanisms.
- Ad Hoc Routing: Reactive (DSR) - On-demand routing alternative
- Ad Hoc Routing: Hybrid (ZRP) - Combining proactive and reactive approaches
- DSDV Evaluation and Trade-offs - Drawbacks and worked examples
