364  WSN Coverage Algorithms

NoteKey Concepts

• Crossing Coverage Theory: Zhang-Hou theorem proving that checking finite crossing points verifies infinite area coverage
• OGDC Algorithm: Optimal Geographical Density Control - distributed algorithm achieving near-optimal triangular lattice coverage
• Virtual Force Algorithm: Coverage repair using simulated attractive/repulsive forces for mobile sensor repositioning
• Coverage Hole Detection: Identifying uncovered regions using Voronoi diagrams and crossing analysis
• Rotation Scheduling: Alternating active sensor sets to extend network lifetime while maintaining coverage

364.1 Learning Objectives

By the end of this chapter, you will be able to:

• Apply Crossing Theory: Use Zhang-Hou theorem to verify coverage with finite checks
• Implement OGDC: Design distributed coverage algorithms with optimal triangular lattice spacing
• Analyze Virtual Force: Understand how mobile sensors use simulated physics for coverage repair
• Design Rotation Schedules: Create energy-efficient coverage maintenance strategies

TipMVU: Minimum Viable Understanding

Core concept: Coverage verification reduces from checking infinite points to finite crossings using Zhang-Hou theorem. Why it matters: OGDC achieves 95%+ coverage with only 40-60% of sensors active, extending network lifetime 2-3x. Key takeaway: Optimal sensor spacing is sqrt(3) x Rs (triangular lattice) - memorize this for deployment planning.

364.2 Prerequisites

Before diving into this chapter, you should be familiar with:

• WSN Coverage Fundamentals: Coverage definitions and connectivity concepts
• WSN Coverage Types: Area, point, and barrier coverage problems

NoteRelated Chapters

Fundamentals: - WSN Coverage Fundamentals - Coverage basics and connectivity - WSN Coverage Types - Area, point, and barrier coverage

Implementations: - WSN Coverage Implementations - Hands-on labs and Python code

Review: - WSN Coverage Review - Comprehensive coverage quiz and summary

364.3 Coverage Maintenance Algorithms

~15 min | Intermediate | P05.C29.U03

364.3.1 Crossing Coverage Theory

Figure 364.1: Crossings in sensor coverage - points where sensing ranges of multiple sensors intersect, critical for ensuring complete area coverage

Figure 364.2: Example of uncovered crossings in sensor network - gaps in coverage occur when sensor ranges do not overlap at boundary points

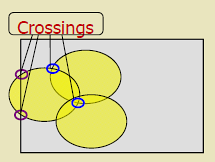
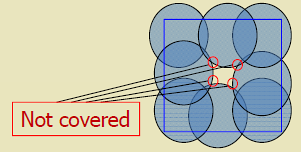
Theorem (Zhang and Hou):

A continuous region is completely covered if and only if: 1. There exist crossings in the region 2. Every crossing is covered

Definitions:

Crossing:

Intersection point between: - Two sensor coverage disk boundaries, OR - Monitored space boundary and a disk boundary

%% fig-alt: "Crossing-based coverage verification showing how checking finite crossing points (sensor boundary intersections) verifies coverage of infinite area points"
%%{init: {'theme': 'base', 'themeVariables': {'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ECF0F1', 'fontSize': '16px'}}}%%
graph TD
    subgraph "Crossing-Based Coverage Verification"
        REGION["Monitored<br/>Region A"]

        CROSS1["Crossing 1<br/>(S1 intersect S2)"]
        CROSS2["Crossing 2<br/>(S2 intersect S3)"]
        CROSS3["Crossing 3<br/>(S1 intersect boundary)"]
        CROSS4["Crossing 4<br/>(S3 intersect boundary)"]

        CHECK{"All crossings<br/>covered?"}

        COVERED["Complete<br/>Coverage"]
        GAPS["Coverage<br/>Holes"]
    end

    REGION --> CROSS1
    REGION --> CROSS2
    REGION --> CROSS3
    REGION --> CROSS4

    CROSS1 --> CHECK
    CROSS2 --> CHECK
    CROSS3 --> CHECK
    CROSS4 --> CHECK

    CHECK -->|"Yes"| COVERED
    CHECK -->|"No"| GAPS

    COVERED -.-> THEOREM["Zhang-Hou Theorem:<br/>Finite crossings<br/>verify infinite points"]
    GAPS -.-> REPAIR["Identify uncovered<br/>crossings for repair"]

    CHECK -.->|"Complexity:<br/>O(N squared) crossings<br/>vs infinite points"| EFFICIENT["Efficient<br/>verification"]

    style REGION fill:#2C3E50,stroke:#16A085,stroke-width:3px,color:#fff
    style CROSS1 fill:#E67E22,stroke:#2C3E50,stroke-width:2px,color:#fff
    style CROSS2 fill:#E67E22,stroke:#2C3E50,stroke-width:2px,color:#fff
    style CROSS3 fill:#E67E22,stroke:#2C3E50,stroke-width:2px,color:#fff
    style CROSS4 fill:#E67E22,stroke:#2C3E50,stroke-width:2px,color:#fff
    style CHECK fill:#3498DB,stroke:#2C3E50,stroke-width:3px,color:#fff
    style COVERED fill:#D5F4E6,stroke:#16A085,stroke-width:3px
    style GAPS fill:#FADBD8,stroke:#E74C3C,stroke-width:3px
    style THEOREM fill:#ECF0F1,stroke:#2C3E50,stroke-width:2px
    style REPAIR fill:#ECF0F1,stroke:#2C3E50,stroke-width:2px
    style EFFICIENT fill:#D5F4E6,stroke:#16A085,stroke-width:2px

Figure 364.3: Crossing-based coverage verification showing how checking finite crossing points verifies coverage of infinite area

Why Crossings Matter:

If all crossings are covered, then all points are covered. This reduces the coverage verification problem from checking infinite points to checking finite crossings.

NoteKnowledge Check: Coverage Hole Detection

viewof kcWsnCov6 = {
  const container = html`<div id="kc-wsn-cov-6-container"></div>`;
  if (container && typeof InlineKnowledgeCheck !== 'undefined') {
    container.innerHTML = '';
    container.appendChild(InlineKnowledgeCheck.create({
      question: "A deployed WSN has 200 sensors with Rs = 15m covering a 300m x 300m area. You need to verify complete coverage. Testing every point in the continuous 90,000 m squared area is impossible. What is the most efficient approach using crossing-based coverage theory?",
      options: [
        {text: "Sample 1000 random points and check if each is within Rs of at least one sensor - statistical approach", correct: false, feedback: "Incorrect. Random sampling provides probabilistic coverage estimation but no guarantees. You might achieve 99% coverage verification confidence, yet miss critical gaps between sample points. For deployed systems requiring coverage guarantees, probabilistic approaches are insufficient."},
        {text: "Compute all crossing points (sensor-sensor and sensor-boundary intersections), verify each crossing is covered - Zhang-Hou crossing theorem", correct: true, feedback: "Correct! Crossing-based verification is the optimal approach: (1) Identify all crossing points: N sensors create O(N squared) sensor-sensor crossings plus O(N) boundary crossings, (2) Verify coverage: Check if each crossing point lies within Rs of at least one sensor, (3) Zhang-Hou Theorem: If all crossings are covered, then ALL points in the region are covered. This deterministic approach guarantees 100% verification with computational feasibility."},
        {text: "Divide area into 1m x 1m grid cells (90,000 cells), check if each cell center is covered - grid approximation", correct: false, feedback: "Incorrect. While grid sampling is better than random sampling, it's still an approximation with potential gaps. A 1m grid with Rs=15m sensors seems safe, but coverage holes smaller than grid resolution go undetected. Additionally, 90,000 cell checks are computationally expensive compared to ~40,000 crossing checks."},
        {text: "Trust the deployment plan - if sensors were placed according to optimal triangular lattice spacing, coverage is guaranteed", correct: false, feedback: "Incorrect. Deployment plans assume ideal conditions that rarely occur in practice: GPS placement errors, sensors falling into obstructed areas, sensor failures during deployment. Post-deployment verification is essential for reliable systems."}
      ],
      difficulty: "hard",
      topic: "coverage-hole-detection"
    }));
  }
  return container;
}

364.3.2 Optimal Geographical Density Control (OGDC)

Figure 364.4: Optimal Geographical Density Control (OGDC) algorithm overview - distributed coverage algorithm that activates minimal sensors while ensuring complete area coverage

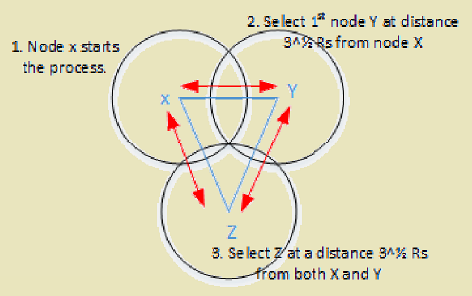
OGDC is a distributed, localized algorithm that achieves near-optimal coverage with minimal active sensors.

Key Idea:

Nodes self-organize into a triangular lattice pattern, which is provably near-optimal for disk coverage.

Optimal Spacing:

For sensors with sensing range Rs, optimal spacing between active sensors is:

\[ d_{optimal} = \sqrt{3} \cdot R_s \]

This minimizes overlap while maintaining complete coverage.

%% fig-alt: "OGDC triangular lattice formation showing optimal sqrt(3) x Rs spacing between active nodes for near-optimal coverage with minimal overlap"
%%{init: {'theme': 'base', 'themeVariables': {'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ECF0F1', 'fontSize': '16px'}}}%%
graph TD
    subgraph "OGDC Triangular Lattice Formation"
        START["Starting Node<br/>(Volunteer)"]

        N1["Node 1<br/>Distance: sqrt(3) x Rs"]
        N2["Node 2<br/>Distance: sqrt(3) x Rs"]
        N3["Node 3<br/>Distance: sqrt(3) x Rs"]
        N4["Node 4<br/>Distance: sqrt(3) x Rs"]
        N5["Node 5<br/>Distance: sqrt(3) x Rs"]
        N6["Node 6<br/>Distance: sqrt(3) x Rs"]

        SLEEP1["Sleeping nodes<br/>(Energy conservation)"]
    end

    START --> N1
    START --> N2
    START --> N3
    START --> N4
    START --> N5
    START --> N6

    N1 -.->|"sqrt(3) x Rs spacing"| N2
    N2 -.->|"sqrt(3) x Rs spacing"| N3
    N3 -.->|"sqrt(3) x Rs spacing"| N4
    N4 -.->|"sqrt(3) x Rs spacing"| N5
    N5 -.->|"sqrt(3) x Rs spacing"| N6
    N6 -.->|"sqrt(3) x Rs spacing"| N1

    START -.-> SLEEP1

    LATTICE["Triangular Lattice<br/>Near-optimal coverage<br/>Minimal overlap"]

    N3 --> LATTICE
    N4 --> LATTICE

    BENEFIT["Benefits:<br/>95% coverage<br/>40-60% nodes active<br/>2-2.5x lifetime"]

    LATTICE -.-> BENEFIT

    style START fill:#E67E22,stroke:#2C3E50,stroke-width:3px,color:#fff
    style N1 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style N2 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style N3 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style N4 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style N5 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style N6 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style SLEEP1 fill:#95A5A6,stroke:#2C3E50,stroke-width:2px,color:#fff
    style LATTICE fill:#3498DB,stroke:#2C3E50,stroke-width:3px,color:#fff
    style BENEFIT fill:#D5F4E6,stroke:#16A085,stroke-width:2px

Figure 364.5: OGDC triangular lattice formation showing optimal sqrt(3) x Rs spacing between active nodes

364.3.3 OGDC Algorithm Phases

Figure 364.6: OGDC Coverage Patterns - Demonstrating how OGDC algorithm progressively activates sensors to achieve full coverage with minimal active nodes

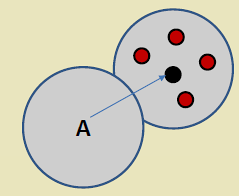
Phase 1: Starting Node Selection

Figure 364.7: OGDC Starting Node Selection - Exponential backoff mechanism to randomly select initial active sensor

def ogdc_select_starting_node(nodes, volunteer_probability=0.1):
    """
    Phase 1: Randomly select starting node using exponential backoff
    """
    for node in nodes:
        if random.random() < volunteer_probability:
            # Volunteer to be starting node
            backoff_time = random.uniform(0, MAX_BACKOFF)
            node.backoff_timer = backoff_time

    # Node with shortest backoff becomes starting node
    time.sleep(max(n.backoff_timer for n in nodes))

    # First node whose timer expires wins
    starting_node = min(nodes, key=lambda n: n.backoff_timer)

    starting_node.activate()
    starting_node.broadcast_start_message()

    return starting_node

class StartMessage:
    def __init__(self, sender_id, sender_position, preferred_direction):
        self.sender_id = sender_id
        self.position = sender_position
        self.direction = preferred_direction  # Random angle 0-360 degrees

Phase 2: Iterative Node Activation

Figure 364.8: OGDC Phase 2 Iterative Activation - Additional sensors activated based on power-off messages from neighbors to maintain coverage

364.3.4 OGDC Performance

Coverage Quality: - Achieves >95% coverage with ~60% of nodes - Near-optimal (within 5% of theoretical minimum)

Energy Efficiency: - 40-60% nodes sleep at any time - Network lifetime extends by 1.67-2.5x

Scalability: - Distributed: No central coordinator - Localized: Only neighbor communication - Scales to thousands of nodes

NoteKnowledge Check: OGDC Algorithm

viewof kcWsnCov7 = {
  const container = html`<div id="kc-wsn-cov-7-container"></div>`;
  if (container && typeof InlineKnowledgeCheck !== 'undefined') {
    container.innerHTML = '';
    container.appendChild(InlineKnowledgeCheck.create({
      question: "A randomly deployed WSN has 300 sensors scattered over agricultural land. Using OGDC algorithm, the system activates 120 sensors achieving 97% coverage, while 180 sensors remain sleeping. The active set provides 8 months lifetime. How should you extend network lifetime to 24 months?",
      options: [
        {text: "Run OGDC once at deployment, keep the same 120 sensors active for entire lifetime - OGDC already optimized the network", correct: false, feedback: "Incorrect. Keeping the same 120 sensors active for 8 months, then replacing them is wasteful. You have 180 unused sleeping sensors that could share the coverage workload. With 300 total sensors and 120 needed per round, you can create 2.5 coverage rounds (300/120 = 2.5), extending lifetime to 20 months through rotation."},
        {text: "Implement coverage rotation: Run OGDC to create 2-3 non-overlapping coverage sets, rotate activation every 8 months leads to ~20-24 month lifetime", correct: true, feedback: "Correct! Coverage rotation with OGDC maximizes lifetime: (1) Round 1: Run OGDC, activate Set A (120 sensors) for 8 months, (2) Round 2: Exclude Set A nodes, run OGDC again on remaining 180 sensors, activate Set B (120 sensors) for 8 months, (3) Round 3: Run OGDC on remaining 60 sensors + reuse some Set A sensors to create Set C (120 sensors) for 4-8 months. Total lifetime: 8 + 8 + 4-8 = 20-24 months vs 8 months (2.5-3x improvement)."},
        {text: "Reduce sensing range Rs to 50% - smaller coverage circles need fewer active sensors, saving energy", correct: false, feedback: "Incorrect. Most sensors cannot dynamically adjust sensing range (Rs is hardware-determined). Even if possible, reducing Rs creates coverage holes - the original 97% coverage with Rs would become 60-70% with 0.5 x Rs (coverage area scales with Rs squared)."},
        {text: "Activate all 300 sensors simultaneously - more sensors mean better coverage and longer lifetime through redundancy", correct: false, feedback: "Incorrect. Activating all 300 sensors would drastically shorten lifetime, not extend it. If 120 sensors provide 8 months lifetime, activating 300 sensors (2.5x energy consumption) would reduce lifetime to 8/2.5 = 3.2 months."}
      ],
      difficulty: "medium",
      topic: "ogdc-coverage-rotation"
    }));
  }
  return container;
}

364.3.5 Virtual Force Algorithm

Virtual force algorithms (Zou and Chakrabarty, 2003) improve coverage through simulated physics:

Algorithm Components:

1. Repulsive forces: Sensors too close together (overlapping coverage) repel each other, spreading out to reduce redundancy. Force is proportional to 1/distance squared.

2. Attractive forces: Coverage holes exert attractive force on nearby sensors, pulling them toward uncovered regions.

3. Boundary forces: Virtual obstacles at deployment boundaries prevent sensors from moving outside target area.

4. Equilibrium: System iterates until forces balance, reaching stable configuration with improved coverage.

%% fig-alt: "Virtual force algorithm showing repulsive forces between nearby sensors and attractive forces from coverage holes"
%%{init: {'theme': 'base', 'themeVariables': {'primaryColor': '#2C3E50', 'primaryTextColor': '#fff', 'primaryBorderColor': '#16A085', 'lineColor': '#16A085', 'secondaryColor': '#E67E22', 'tertiaryColor': '#ECF0F1', 'fontSize': '16px'}}}%%
graph TD
    subgraph "Virtual Force Algorithm"
        S1["Sensor S1"]
        S2["Sensor S2<br/>(Too close)"]
        S3["Sensor S3"]

        HOLE["Coverage<br/>Hole"]

        BOUNDARY["Deployment<br/>Boundary"]
    end

    S1 <-->|"Repulsive<br/>Force"| S2
    S2 <-->|"Repulsive<br/>Force"| S3

    HOLE -.->|"Attractive<br/>Force"| S1
    HOLE -.->|"Attractive<br/>Force"| S3

    BOUNDARY -.->|"Boundary<br/>Force"| S1
    BOUNDARY -.->|"Boundary<br/>Force"| S3

    RESULT["Equilibrium:<br/>Sensors spread out<br/>Holes filled<br/>Stay in bounds"]

    S1 --> RESULT
    S2 --> RESULT
    S3 --> RESULT

    style S1 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style S2 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style S3 fill:#16A085,stroke:#2C3E50,stroke-width:3px,color:#fff
    style HOLE fill:#E74C3C,stroke:#2C3E50,stroke-width:3px,color:#fff
    style BOUNDARY fill:#7F8C8D,stroke:#2C3E50,stroke-width:2px,color:#fff
    style RESULT fill:#D5F4E6,stroke:#16A085,stroke-width:2px

Figure 364.9: Virtual force algorithm showing repulsive forces spreading sensors apart and attractive forces pulling them toward coverage holes

Algorithm Steps:

For each sensor: 1. Calculate forces from all neighbors (repulsive) and coverage holes (attractive) 2. Compute net force vector 3. Move sensor incrementally in force direction 4. Repeat until convergence (forces below threshold)

Requirements: Mobile sensors with locomotion capability (wheeled robots, aerial drones). Not applicable to static sensors.

Performance: Improves random deployment coverage from 75% to 95% through iterative repositioning.

Costs: - Mobility hardware: Expensive and energy-intensive - Localization: Sensors must know their positions (GPS, trilateration) - Computation: Force calculations require neighbor positions

Applications: Underwater sensor networks (AUVs can relocate), aerial drone swarms, disaster response robots. Not practical for scattered static sensors.

Alternative for static networks: Use virtual forces to plan initial deployment, then execute with static sensors.

NoteKnowledge Check: Virtual Force Algorithm

viewof kcWsnCov9 = {
  const container = html`<div id="kc-wsn-cov-9-container"></div>`;
  if (container && typeof InlineKnowledgeCheck !== 'undefined') {
    container.innerHTML = '';
    container.appendChild(InlineKnowledgeCheck.create({
      question: "A disaster response team deploys 50 mobile drone sensors after an earthquake. Initial random landing achieves only 72% coverage of the search area. Coverage holes exist in critical zones. Which strategy should improve coverage most effectively?",
      options: [
        {text: "Manual repositioning - operators fly each drone to predetermined grid positions based on aerial survey", correct: false, feedback: "Incorrect. Manual repositioning is slow (operator must control each drone individually), error-prone (GPS inaccuracy, operator fatigue), and doesn't adapt to terrain obstacles. For 50 drones, manual positioning could take hours. Virtual force algorithm autonomously repositions all drones simultaneously in minutes, adapting to discovered obstacles and coverage gaps in real-time."},
        {text: "Virtual force algorithm - drones simulate repulsive forces to spread out and attractive forces toward coverage holes until equilibrium", correct: true, feedback: "Correct! Virtual force algorithm is optimal for mobile sensor coverage repair: (1) Distributed: Each drone calculates local forces from neighbors and coverage holes, (2) Autonomous: No central coordinator needed, scales to large swarms, (3) Adaptive: Drones avoid obstacles and terrain by treating them as boundary forces, (4) Convergence: System reaches equilibrium in 10-20 iterations (5-10 minutes for drone network). Expected improvement: 72% to 90%+ coverage through autonomous repositioning."},
        {text: "OGDC algorithm - run OGDC to determine which drones should be active and which should sleep", correct: false, feedback: "Incorrect. OGDC is designed for static sensor networks with redundant deployment - it selects which sensors to activate, not where to move them. In disaster response with 50 drones and 72% coverage, you don't have redundant sensors to put to sleep - you need to move existing sensors to fill coverage holes. OGDC optimizes activation scheduling; virtual force optimizes sensor positions."},
        {text: "Deploy additional drones - 72% coverage is insufficient; add 30 more drones to achieve 95%+ coverage", correct: false, feedback: "Incorrect. Adding drones is expensive (hardware cost, logistics of transporting additional drones to disaster zone) and may not be feasible in emergency situations. The 50 existing drones can likely achieve 90%+ coverage if properly positioned - the problem is placement, not quantity. Random landing created clusters and gaps; virtual force repositioning spreads drones optimally without additional hardware."}
      ],
      difficulty: "medium",
      topic: "virtual-force-coverage-repair"
    }));
  }
  return container;
}

364.4 Algorithm Comparison

Algorithm	Type	Coverage	Active Sensors	Complexity	Best For
Crossing Theory	Verification	100% verified	N/A	O(N squared)	Coverage checking
OGDC	Activation	95-98%	40-60%	O(N log N)	Static WSN
Virtual Force	Repositioning	90-95%	100%	O(N squared)	Mobile sensors
Grid Deployment	Placement	100%	100%	O(1)	Accessible terrain

364.5 Summary

This chapter covered three key coverage algorithms:

Key Takeaways:

1. Crossing Theory - Zhang-Hou theorem enables efficient coverage verification by checking O(N squared) crossing points instead of infinite area points.

2. OGDC Algorithm - Distributed, localized algorithm achieving near-optimal triangular lattice (sqrt(3) x Rs spacing) with 40-60% energy savings.

3. Virtual Force - Mobile sensor repositioning using simulated physics (repulsive between sensors, attractive toward holes). Best for drone swarms and disaster response.

4. Algorithm Selection - Use crossing theory for verification, OGDC for static WSN activation, virtual force for mobile sensor coverage repair.

364.6 What’s Next?

Now that you understand coverage algorithms, the next chapter provides hands-on labs and Python implementations.

Continue to WSN Coverage Implementations - Build and test coverage systems with practical labs and code examples.