231 Processes and Systems: PID Control
231.1 Overview
This section covers PID (Proportional-Integral-Derivative) control, the most widely used feedback control algorithm in industrial and IoT applications. PID controllers enable precise, automated control of processes ranging from temperature regulation to motor speed control.
231.2 What You’ll Learn
The PID control content is organized into three focused chapters:
231.2.1 Part 1: PID Control Fundamentals
Learn the foundation of PID control:
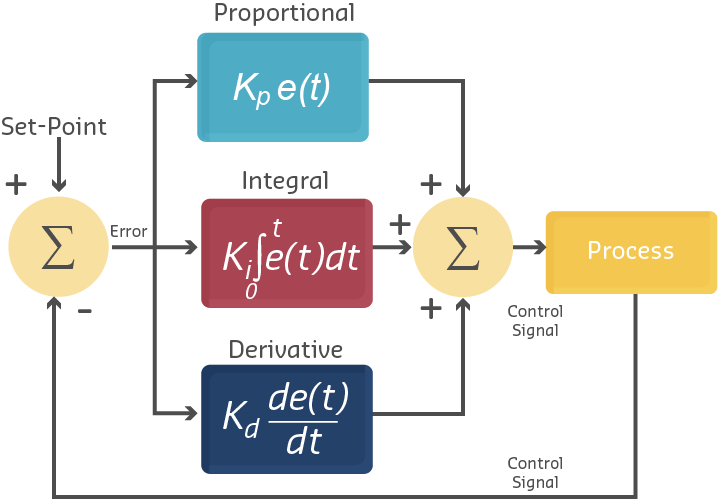
- PID Components: Understanding the three terms (P, I, D) and their roles
- Error Calculation: How setpoint, process variable, and error relate
- Proportional Control: How P-term responds to current error magnitude
- P-Only Limitations: Why proportional control alone causes steady-state error
- PID Equation: The mathematical foundation for controller output
231.2.2 Part 2: Integral and Derivative Control
Master the I and D terms:
- Integral Control: Eliminating steady-state error through error accumulation
- Integral Windup: Preventing dangerous over-accumulation
- Derivative Control: Using rate of change to reduce overshoot
- PID Configuration Selection: When to use P, PI, PID, or PD
- Tuning Philosophy: Why conservative gains outperform aggressive tuning
231.2.3 Part 3: PID Implementation and Labs
Hands-on implementation:
- Arduino/ESP32 Code: Complete PID controller class in C++
- Lab Exercises: Systematic tuning exploration with P, PI, and PID
- Python Framework: Production-ready simulation and auto-tuning
- Performance Metrics: Measuring settling time, overshoot, and error
- Distributed Control: Edge vs cloud control architecture decisions
231.3 Prerequisites
Before starting this section, you should understand:
- Basic feedback control concepts (open-loop vs closed-loop)
- Process variables, setpoints, and error signals
- Simple programming concepts (variables, loops, functions)
231.4 Learning Path
| Chapter | Focus | Difficulty | Time |
|---|---|---|---|
| PID Fundamentals | Theory & P-term | Intermediate | 25 min |
| Integral & Derivative | I & D terms | Intermediate | 30 min |
| Implementation | Code & Labs | Advanced | 45 min |
231.5 Quick Reference
PID Equation: \[ u(t) = K_p \cdot e(t) + K_i \cdot \int_{0}^{t} e(\tau) \, d\tau + K_d \cdot \frac{de(t)}{dt} \]
Common Configurations:
| Mode | When to Use |
|---|---|
| P | Simple systems, some error acceptable |
| PI | Most common, general-purpose control |
| PID | High-performance, minimal overshoot needed |
| PD | Fast servos without steady-state concerns |
231.6 Start Learning
Recommended: Begin with PID Control Fundamentals for a solid foundation.
Advanced: Jump directly to Implementation and Labs if you already understand PID theory.
